Wartość bezwzględna jest liczbą, która zapisywana jest w postaci:
|x|
co czytamy jako:
wartość bezwzględna z liczby x
Wartość bezwzględna z liczby dodatniej będzie zawsze równa liczbie znajdującej się w wartości bezwzględnej. Spójrz na przykłady poniżej:
|7| = 7
|10| = 10
|4 + 8| = |12| = 12
|√2 + 2| = √2 + 2Wartość bezwzględna z liczby ujemnej będzie zawsze równa liczbie przeciwnej znajdującej się w wartości bezwzględnej. Spójrz na przykłady poniżej:
|-6| = -(-6) = 6
|-15| = -(-15) = 15
|15 – 20| = |-5|= -(-5) = 5
|√2 – 4| = -(√2 – 4) = -√2 + 4Definicja wartości bezwzględnej
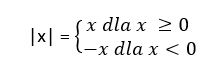
Jak rozumieć powyższy zapis? Otóż:
wyrażenie w wartości bezwzględnej nie zmienia swojego znaku, jeśli to co stoi w wartości bezwzględnej jest większe lub równe zero. Czyli mówimy tu o pierwszym warunku:
|x| = x dla x ≥ 0co można przedstawić w przykładzie:
|25| = 25, ponieważ spełniony jest powyższy warunek, czyli 25 ≥ 0
oraz
wyrażenie w wartości bezwzględnej zmienia swój znaku na przeciwny, jeśli to co stoi w wartości bezwzględnej jest mniejsze od zera. Czyli mówimy tu o pierwszym warunku:
|x| = -x jeśli x < 0
co można przedstawić w przykładzie:
|-120| = 120, ponieważ -120 < 0
Geometryczna interpretacja wartości bezwzględnej
Wartość bezwzględną interpretuje się graficznie, ponieważ wartość bezwzględna to odległość na osi liczbowej między dwiema liczbami.
Wyrażenie |3| można zapisać jako |3 – 0| co ilość jednostek na na osi liczbowej między liczbą 3 a 0. Zobacz:

Między zerem a trójką znajdują się trzy jednostki na osi liczbowej, dlatego |3| = 3.
Zobacz na następujący przykład:
|-4|
w tym przypadku wyrażenie to również możemy zapisać jako |-4 – 0|, co oznacza ilość jednostek na osi liczbowej miedzy liczbą -4 a zerem. Zobacz na wykres:

między liczbą -4 a 0 na osi liczbowej są 4 jednostki, stąd
|-4| = 4
Z powyższych dowodów wynika, że wartość bezwzględna nie może być liczbą mniejszą od zera, ponieważ odległość na osi liczbowej między dwiema liczbami również nie może być mniejsza od zera.
Na temat definicji wartości bezwzględnej mówię na swoim kanale, gdzie wyjaśniam, czym jest wartość bezwzględna i omawiam przykłady praktyczne 
Jeśli jesteś zainteresowany innymi przykładami, to koniecznie przejdź dalej i rozwiąż zadania, które zamieszczam poniżej. Pod każdym zadaniem znajdziesz link do rozwiązania wideo
Część I
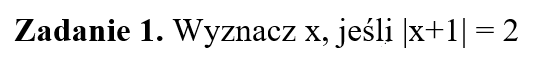
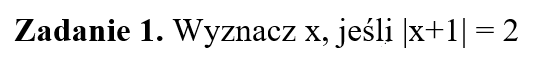
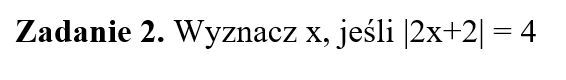
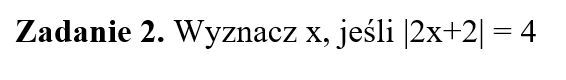
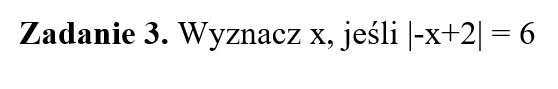
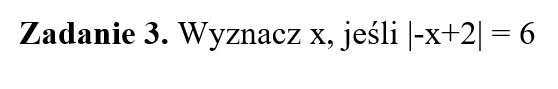
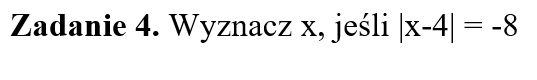
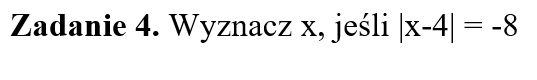
Dlaczego warto korzystać z interpretacji algebraicznej wartości bezwzględnej podczas rozwiązywania tego 👆 typu równań?
Odpowiedź znajdziesz w poniższym filmie 👇
Część II
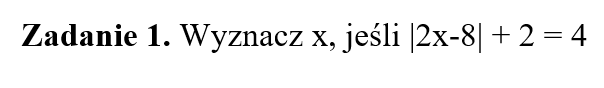
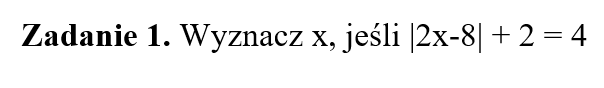
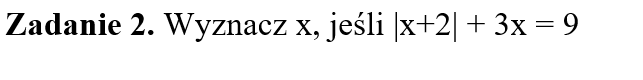
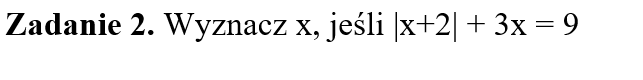
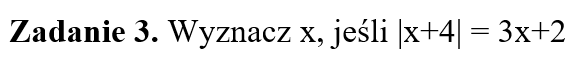
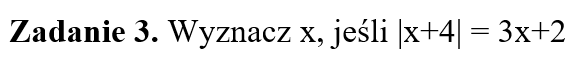
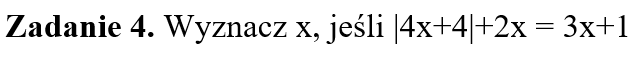
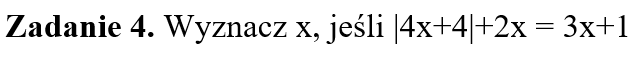
Część III
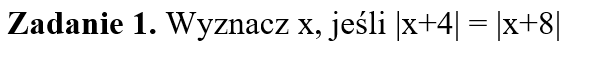
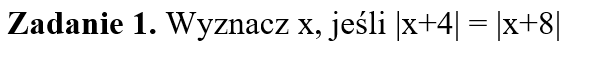
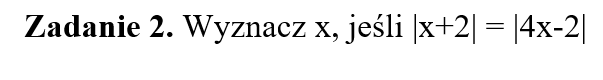
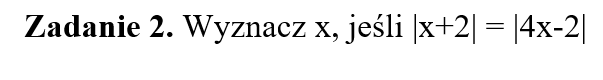
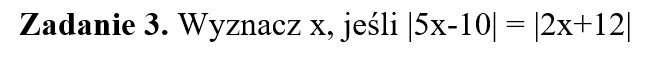
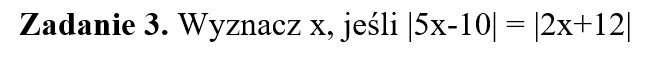
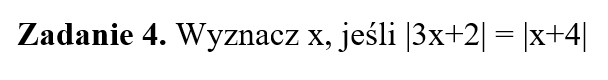
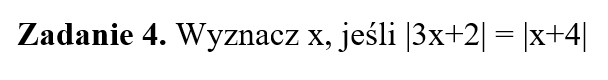
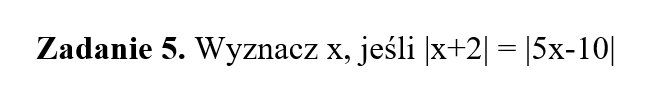
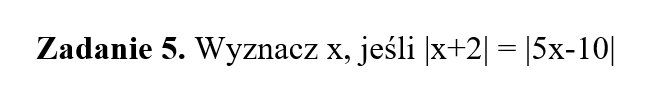
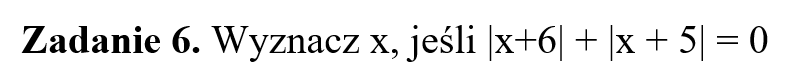
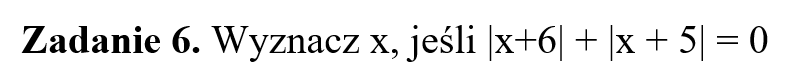
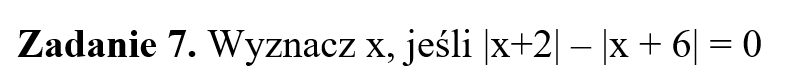
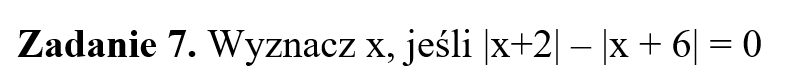
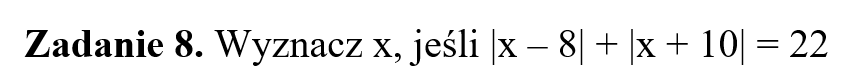
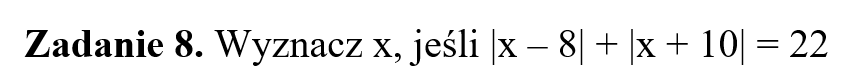
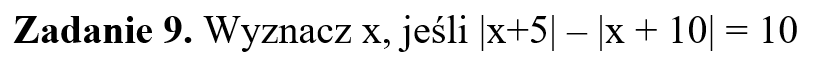
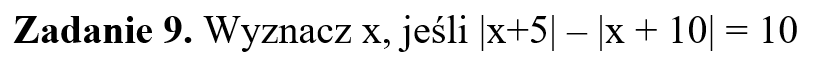
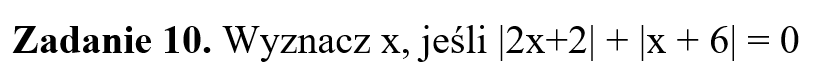
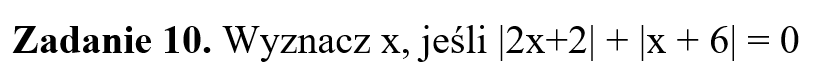
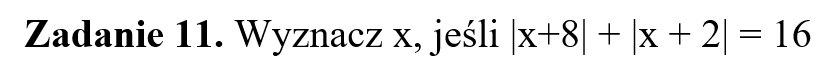
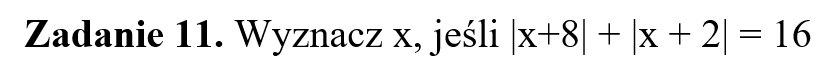
Część IV
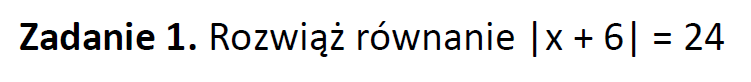
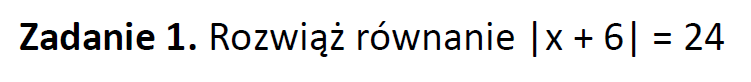
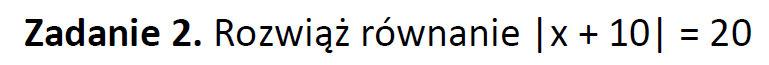
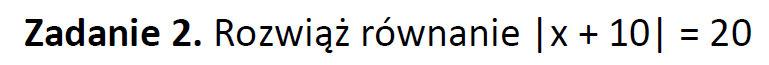




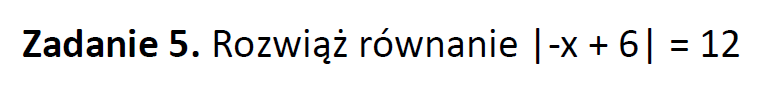
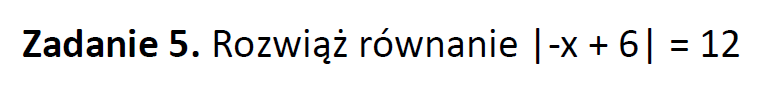


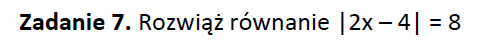
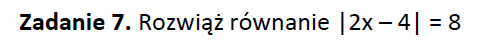






Część V
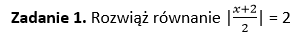
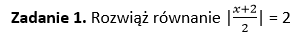
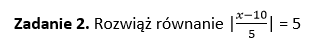
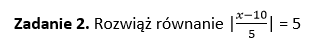
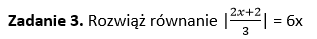
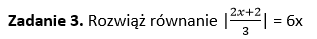
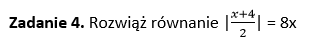
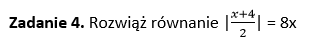



[…] 👉 Równania z wartością bezwzględną […]