Ciąg geometryczny to taki ciąg, którego każdy kolejny wyraz jest q razy większy od poprzedniego lub q razy mniejszy od poprzedniego. Przy czym liczbę q nazywamy ilorazem ciągu geometrycznego.
Z definicji ciągu geometrycznego wyniki, że każdy kolejny wyraz ciągu geometrycznego mnożymy przez liczbę q.
Popatrz na przykłady.
Przykład 1.
2; 4; 8; 16; 32; …….
tutaj q = 2, ponieważ każdy kolejny wyraz ciągu jest dwa razy większy od poprzedniego. Jest to zatem ciąg rosnący.
Przykład 2.
2; -4; -8; 16; -32; …….
tutaj q = 12, ponieważ każdy kolejny wyraz ciągu jest dwa razy większy od poprzedniego. Jest to zatem ciąg niemonotoniczny, ponieważ nie jest to ciąg ani rosnący, ani malejący ani stały
Przykład 3.

tutaj ![]() , ponieważ każdy kolejny wyraz ciągu jest “pół razy większy od poprzedniego”, czyli w gruncie rzeczy o połowę mniejszy od poprzedniego. Każdy kolejny wyraz ciągu mnożony jest tu przez
, ponieważ każdy kolejny wyraz ciągu jest “pół razy większy od poprzedniego”, czyli w gruncie rzeczy o połowę mniejszy od poprzedniego. Każdy kolejny wyraz ciągu mnożony jest tu przez ![]() . Jest to ciąg malejący.
. Jest to ciąg malejący.
Aby można było ocenić, czy ciąg jest geometryczny, ciąg ten musi być minimum trzy-elementowy. Dlaczego? Popatrzmy na ciąg poniżej:
2; 4
Tu nie mamy możliwości ocenić, czy do liczby 2 dodajemy 2 (wtedy byłby to ciąg arytmetyczny), czy liczbę 2 mnożymy przez 2 (wtedy byłby to ciąg geometryczny). Natomiast popatrz na ciąg poniżej:
2; 4; 8
tu nie ma wątpliwości, że jest to ciąg geometryczny.
Z ciągiem geometrycznym związanych jest kilka wzorów, których znajomość jest niezbędna do rozwiązywania zadań. Oto najważniejsze z nich, które każdy maturzysta znać powinien.
Kolejny wyraz ciągu geometrycznego powstaje przez pomnożenie poprzedniego wyrazu przez pewną stałą wartość, zwaną ilorazem ciągu. Możemy zapisać to następująco:

n-ty wyraz ciągu geometrycznego obliczamy ze wzoru:

Aby obliczyć sumę n – początkowych wyrazów ciągu geometrycznego, korzystamy z jednego z dwóch wzorów:

Własność ciągu geometrycznego:

Zobacz wideo wprowadzające do ciągu geometrycznego 
Ciąg geometryczny – zadania




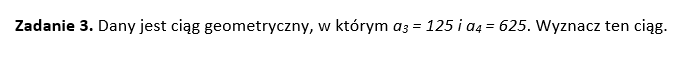
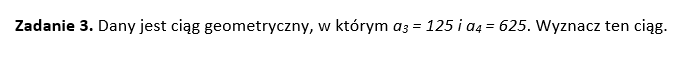




























Zobacz rozwiązanie wideo 









































































[…] 👉 Ciąg geometryczny: https://ilonabednarska.pl/ciag-geometryczny/ […]