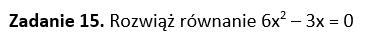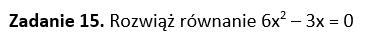Równania kwadratowe
Postać ogólna równania kwadratowego:
ax2 + bx + c = 0
Równania kwadratowe z jedną niewiadomą to równania stopnia drugiego. Równania stopnia drugiego mogą zawierać więcej niż jedną niewiadomą, jednak w tym miejscu nie będziemy się nimi zajmować. Rozwiązanie równań kwadratowych z jedną niewiadomą polega na znalezieniu wartości niewiadomej, jeśli takie istnieją, które spełniają dane równanie.
Co to znaczy, że wartość niewiadomej spełnia dane równanie? Otóż oznacza to tyle, że jeśli wartość niewiadomej podstawimy pod tą niewiadomą, to całe wyrażenie będzie równe zero.
Wartość liczbowa, która jest rozwiązaniem danego równania, także kwadratowego, to jest szukana liczba. Jest ona zwana pierwiastkiem równania.
Aby rozwiązań równanie kwadratowe, należy w pierwszej kolejności wyznaczyć deltę i na podstawie jej wartości ocenić, ile równanie ma pierwiastków.
Równanie kwadratowe może:
- mieć maksymalnie dwa rozwiązania, jeśli wartość delty będzie większa od zera
- mieć dokładnie jedno rozwiązanie, jeśli wartość delty będzie równa zero
- może nie mieć rozwiązań w ogóle, jeśli wartość delty będzie mniejsza od zera
Pierwiastki równania kwadratowego liczymy z tych samych wzorów co miejsca zerowe funkcji kwadratowej
Wysłuchaj nagrania, w którym omawiam zasady rozwiązywania równań kwadratowych z jedną niewiadomą 
Zadanie 1.


Zadanie 2.
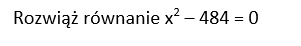
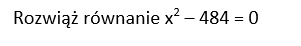
Zadanie 3.
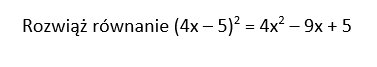
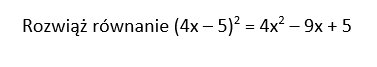
Zadanie 4.


Zadanie 5.


Zadanie 6.


Zadanie 7.


Zadanie 8.
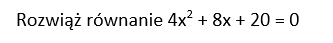
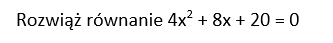
Zadanie 9.